合情联想 创新运用 开心启智
江苏省淮安曙光双语学校 叶士江
“创新是一个民族精神的灵魂,是一个国家兴旺发达的不竭动力。”而“钱学森之问”——为什么我们的学校总是培养不出杰出人才?则深深撕痛国人教育深处之讳——创新教育、运用能力培养的不给力!
如果说数学知识和数学思想方法是数学的核心,那么在这“知识”与“方法”背后所蕴藏的“学生创新和实际运用能力的培养”则一定是学校日常数学教学的孜孜以求。鉴于此,我的数学课堂教学追求的就是“唤醒主体意识,引导联想方法,培养创新能力”。缘于年龄特点,对于小学生而言,我以为培养学生的创新运用能力,主要得依赖于“由此及彼”、“由表及里”式的合情联想,从而让学生在开阔数学视野的过程中,增强学生洞悉日常生活问题中的数学元素或复杂数学问题中的简单“原形”的能力,真正达到在过程中、在实践中培养学生创新运用的境界。试想,如果我们的各科教学、各阶段教育,都一路给力,开心启智,定出培养出钱老所欣赏的成批的“杰出人才”。
现列举我课堂上的四个案例,与同仁们分享孩子们的“发现之旅”。
案例一:联想生活经验,巧解趣题
【问题】大小两个正方形拼成下图1,大正方形ABCD的边长是6cm。连接EC与AD相交于点H,并且DH=2cm。请问小正方形EFDG的面积是多少?
.jpg)
【发现之旅】显然要求小正方形的面积,就必须知道小正方形的边长,可是怎么办呢?
现在我们不妨将三角形EFC暂时从整体中移出来,变成图2来单独研究。静下心来,仔细端详上几眼,是不是产生了联想,有种很熟悉的感觉跳到眼前:EF和HD好比是两棵笔直的“树”矗立在灿烂的阳光下,阳光照来,它们顶端的影子同时落在了C点, FC和DC不就正好分别是它们的影子吗?
从图2中,我们可以很方便地知道“HD”这棵小树的影子正好是它自己高度的6÷2=3倍。联想我们的日常生活经验,同一时间、同一地点,“树”的高度与它的影子是成正比例的,所以树“EF”的影子FC的长也应该是自己高度EF长的3倍,而很明显FD=EF,因此很容易得出DC=2EF,而DC=6cm,所以小正方形的边长EF=6÷2=3(cm)。
现在,可以很轻松地求出小正方形EFDG的面积是:32=9(cm2)
案例二:联想学习经历,巧解趣题
【问题】等腰梯形ABCD的对角线AC长20cm,并且∠ACB=450 (如图3)。这个梯形的面积是多少?
.jpg)
【发现之旅】一般来说,求梯形的面积,得知道它的上、下底和高,但此题这些一概不知,怎么办?可别忽视图3中有一个重要的条件:∠ACB=450。
现在让我们联想以前推导平行四边形面积公式时的做法,先从A点向梯形下底作垂线AE(如图4),再将△ABE切割后旋转移至右边(如图5),拼成的是长方形,还是正方形呢?
分析一下,△AEC其中的一个锐角∠ACE=450,另一个锐角∠CAE也应是450,所以它是个等腰直角三角形,因此AE=EC,显然拼成的四边形AECB是一个正方形。
问题又出来了,AC并不是拼成的正方形的边长,而是它的对角线的长度。再次联想我们以前的学习经历,知道正方形的对角线长度,是如何求它的面积的呢?对,将正方形用两条对角线均分成四个等腰直角三角形(如图6),每个的面积就是:20÷2=10(cm),10×10÷2=50(cm2)。
由此,正方形的面积,也就是原来梯形的面积是:50×4=200(cm2)

案例三:联想具体数字,巧解趣题
【问题】长方形ABCD被分为面积相等的四个部分(如图7),如果AB:BH=3:2,请问DF:FC=?
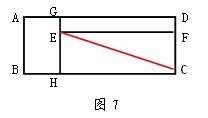
【发现之旅】此题无任何一条线段的具体长度,推理起来显然比较麻烦。根据条件AB:BH=3:2,我们不妨大胆将其联想作为特例:AB=3cm,BH=2cm。这样图7中四个部分的面积都是3×2=6(cm2),现在可以进一步推理:
长方形ABCD的面积是6×4=24(cm2),宽BC=24÷3=8(cm),HC=8-2=6(cm)
三角形CEF中:CF=6×2÷6=2(cm)
小长方形GEFD中:DF=6÷6=1(cm)
至此,可以清楚地得到DF:FC=1:2
(试想:如果将AB和BH分别看作9cm和6cm,结果还会一样吗?)
案例四:联想平面镜子,巧解趣题
【问题】欢欢是幸福村里有名的“敬老小明星”加“数学智多星”,他每天都要从自家(图8中A处)出发去村里的“长寿泉”边打上一担清洁的水送到孤寡老人李爷爷家(图8中B处)。你能画出聪明的欢欢每次所走的最短路线吗?
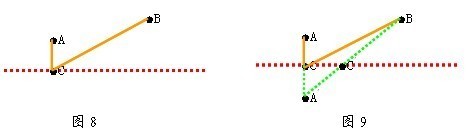
【发现之旅】两点之间线段最短,连接AB不是最短的送水路线吗?显然不是,因为这样没能取到水。是欢欢先垂直地走到C处取水后,再径直送到李爷爷家,走AC→CB的路线是最短吗?(如图8)有点疑问,毕竟走的是“两条线”。
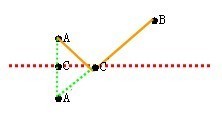
那么,欢欢到底能不能做到:取水、送水走的是“同一条线”呢?这看上去好像不可能,因为欢欢的家不在泉的对岸!现在我们就很自然地能联想到生活中的“镜子”:将“长寿泉”当作一面镜子,先将他的家“照”到对岸的A′处去,AC=A′C。现在,他的家在“A′”处了,连接A′B,与泉岸相交于点C′。欢欢走的路线也就是A′C->C′B,正好是一条线段,当然也就是最短的送水路线了。图9中也可以明显地得出在三角形A′BC中,A′B′C+CB,即A′B
现在我们可以轻松地画出欢欢所走的最短路线就是图10中的从A→C′→B。
作者简介:叶士江,淮安市小学数学骨干教师,国家二级奥林匹克数学教练员,淮安曙光双语学校小学部教科室主任。
最新文章
精品专题
推荐文章